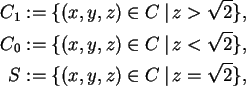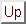

Next:Messung
des ErdumfangsUp:Ringvorlesung
,,Geschichte der Mathematik'' Previous:Vermessung
der Erde
Geometrie der Ideen
 |

iese Überschrift ist so gemeint: Viele Griechen, am ausdrücklichsten
unter ihnen wohl Pythagoras
aus Samos (? - 490 v.Chr.), aber auch Platon
(427 - 347 v.Chr.), haben begründet, daß die Geometrie nicht
von 'wirklichen' Dreiecken, Vierecken, Kreisen usw. handelt, sondern von
idealen, 'gedachten' Figuren. Pythagoras hat erkannt, daß
die Sätze der Geometrie, damit diese als 'wahr' gelten sollen, einen
Beweis brauchen, und wohl beim Herumsuchen, was denn ein guter Beweis sei,
hat er erkannt, daß jeder Beweis vorher Voraussetzungen, faktisch
also Definitionen und Axiome braucht. Mit diesen Ideen hat er eine Schule
(vielleicht fast eine Sekte) gegründet, die dieses Beweisen gepflegt
hat, und die dann -vielleicht durch ihn selbst, oder einen seiner Schüler-
in große sachliche Schwierigkeiten gekommen ist (vgl. Platon's
Menon). |
 |
Wenn man nämlich das Messen von Strecken und Flächen (praktisch
für die Flächensätze des rechtwinkligen Dreiecks) über
den Strahlensatz schließlich sorgfältig definiert, kommt etwas
ganz Wunderliches heraus. Man kann beweisen, daß man die Länge
der Diagonale eines Quadrates gar nicht, wie definiert, messen kann mit
der Einheit, die die Seite des Quadrats innehat, denn 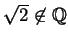 .
Die allereinfachste Konstruktion eines Quadrates schon übersteigt
die Möglichkeiten der griechischen Arithmetik. Platon betont
immer wieder, wie wichtig die Geometrie ist, denn genau damit kann
er zeigen, daß es 'seinen Ideen-Himmel' wirklich geben muß.
.
Die allereinfachste Konstruktion eines Quadrates schon übersteigt
die Möglichkeiten der griechischen Arithmetik. Platon betont
immer wieder, wie wichtig die Geometrie ist, denn genau damit kann
er zeigen, daß es 'seinen Ideen-Himmel' wirklich geben muß.
Das hatte auch inner-mathematisch drastische Folgen: Bei Euklid
ist die ganze Arithmetik in geometrischer Gestalt behandelt, als eine Streckenrechnung,
denn 'Zahlen' sind immer 'Verhältnisse von zwei Strecken'. Daß
man die rationalen Zahlen leicht definieren kann, und daraus auch die reellen
Zahlen (zum Beispiel als Dedekind'sche Schnitte in 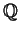 )
hätte die Griechen nie befriedigt. Aber für jene Verhältnis-Rechnung
(nach Eudoxos) ist das überhaupt kein Problem. Denn die Zahlen
)
hätte die Griechen nie befriedigt. Aber für jene Verhältnis-Rechnung
(nach Eudoxos) ist das überhaupt kein Problem. Denn die Zahlen 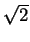 und
und 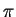 ,,gibt es dann'' ganz offensichtlich. Man braucht so auch keine Mengenlehre
vorab.
,,gibt es dann'' ganz offensichtlich. Man braucht so auch keine Mengenlehre
vorab.
Die Lage für die griechischen Mathematiker war aber gerade deshalb
noch viel komplizierter, und so, daß es auch ,,in modernen Worten''
nicht einfach ist. Wenn man die Gleichheit von Zahlen durch Streckenrechnung
definiert hat, ist eine Frage von Demokritos (459 - 371 v.Chr.)
immer noch nicht glatt zu beantworten (Hermann Diels: Die Fragmente
der Vorsokratiker, Fragment 155):
,,Wenn ein Kegel unmittelbar an der Grundfläche mittels einer Ebene
geschnitten wird, wie soll man sich die entstehenden Schnittflächen
denken, gleich oder ungleich (kongruent oder inkongruent)? Sind sie ungleich,
dann werden sie den Kegel ungleichmäßig machen, da er viele
stufenartige Einschnitte und Vorsprünge erhält; sind sie dagegen
gleich, so werden auch die Schnitte gleich sein, und der Kegel wird die
Erscheinung des Zylinders darbieten, da er aus gleichen, nicht aus ungleichen
Kreisen bestehen wird, was doch sehr ungereimt ist.''
Dieser Widerspruch ist wohl ein elementares Motiv für die Lehre
von den Atomen bei Demokrit gewesen.
Aber wenn man nun geteilt hat, sind notwendig entweder C0
oder C1 oder beide offen und nicht abgeschlossen, und
jede einzelne Fläche in C0 ist kleiner als jede
einzelne Fläche in C1.
Wenn man ,,Gleichheit'' als eine Äquivalenzrelation definiert,
gibt es kein Problem. Aber warum sind C+0
und C-1 denn nun ,,wirklich gleich''?


Next:Messung
des ErdumfangsUp:Ringvorlesung
,,Geschichte der Mathematik'' Previous:Vermessung
der Erde
18.1.1999 �