
Consider the set G3 of all three-dimensional “objects” or “things” (e.g., geometrical bodies, polytropes,...) as closed subsets of threedimensional space IR3. We do not assume anything further on this set, although it appears reasonable to suppose properties like countability or existence of finitely many generating elements (“prototypes”, primitive figures). Let moreover denote F2 the set of two-dimensional “figures”, i.e., closed subsets of the plane IR2, which are representable locally (i.e., on the intersection set with an open subset of IR2) by three-dimensional objects (at least on their intersection set with an open subset of IR3). Consider then the perspective projections
P3,2: G3 —› F2.
G3 thus is something like the “real world.” P3,2 is a well-defined mapping (to every geometric body there exists a figure!). However: It is neither injective (one-to-one) nor surjective (on-to): Firstly, there are many objects represented by the same figure; secondly, there exist two-dimensional figures which are no projections of threedimensional bodies: “impossible figures”. Nonetheless the construction mechanism
K2,3: F2 —› G3
works, given the local mental construction rules, even for these figures. We get the following figure:
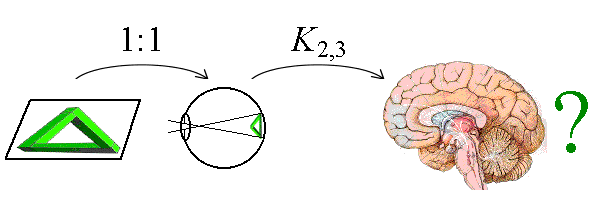
The construction of the third dimension is a n:m-mapping, whereas the mapping of a twodimensional figure on the also twodimensional retina of the eye is a 1:1-mapping (a bijection).